Relatório - Prova Prática 1
Análise de Séries Temporais
Allan Vieira 14/0128492
Junho, 2018
1) Análise da concentração de partículas inaláveis finas (MP\(_{2.5}\)) da cidade de London, província de Ontário, Canadá, no ano de 2013
Contextualização do problema:
O arquivo Matter2013-London.csv, obtido em http://www.airqualityontario.com, contém informações sobre as concentrações de partículas inaláveis finas (MP\(_{2,5}\), em \(\mu g/m^{3}\) ), registradas no ano de 2013 em London, cidade situada na província canadense de Ontário. Os valores são registrados a cada hora. Para determinado dia D, as variáveis \(\textit{H}_{1}\) a \(\textit{H}_{24}\) representam as medições feitas na primeira até a \(24^{ª}\) hora do dia, respectivamente.
O objetivo é realizar uma análise exploratória desta série temporal dada por:
\[Y_{t} = min\{H_{j,t}\},\]
em que \(j = 1,...,24\) e \(H_{j,t}\) representa o valor de MP\(_{2,5}\) observado no dia \(t\) na hora \(H\).
item i)
Dados brutos antes do tratamento:
Dados após preparação:
Gráfico da série temporal \(Y_{t}\):
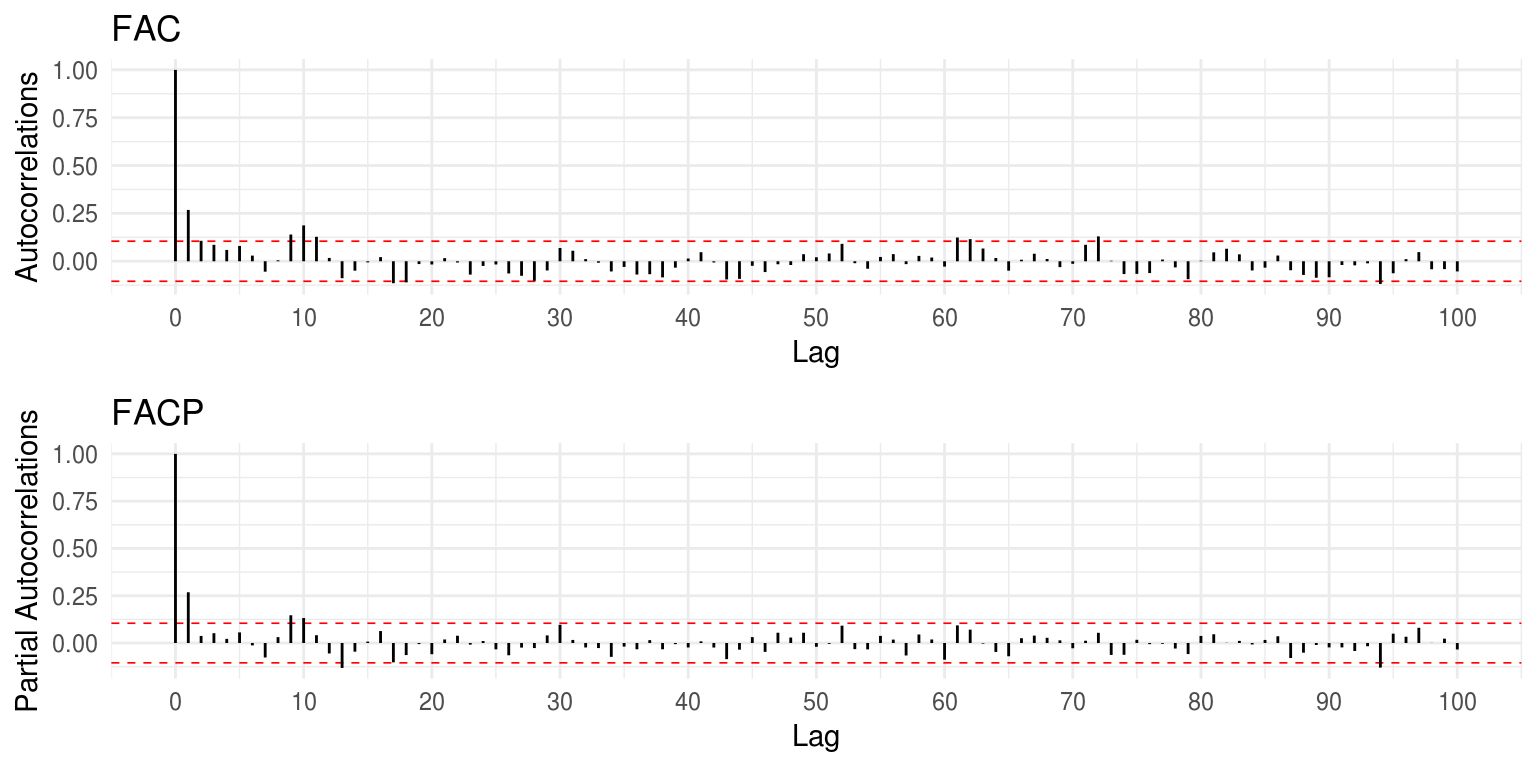
Plots da FAC e FACP:
item ii)
O Gráfico da série não indica ausência de estacionariedade no que se refere a sua média. O gráfico da Função de Autocorrelação (FAC), com \(\rho(1) \sim 0.25\), assim como os valores de \(\rho(h)\) tendendo rapidamente a zero nos lags superiores, parecem indicar a estacionariedade na série.
OBS: optamos por não utilizar o teste de Dick-Fuller, devido às duas funções disponíveis nos pacotes aTSA e tseries do R para este fim estarem apresentando resultados discrepantes, mesmo com o devido ajuste das hipóteses alternativa e nula.
item iii)
Com base no gráfico da FAC, a queda exponencial da autocorrelação nos primeiros lags parece indicar um modelo autorregressivo. A FACP, por sua vez, nos permite inferir a possível ordem deste modelo autorregressivo: como há apenas o lag \(h=1\) acima das bandas de confiança, sugere-se um modelo de filtro linear AR(1) (ou ARIMA(1,0,0)). Valores de autocorrelação acima das bandas de confiança em lags superiores podem ser atribuídos ao percentual esperado de erro tipo I ou tratados como valores espúrios devido a erro amostral.
Poder-se-ia, ainda, utilizar a função auto.arima() do pacote forecast para obter uma sugestão automática acerca do modelo de filtro linear para a série estacionária no caso. A utilização desta função corrobora a sugestão de modelo que fizemos utilizando como base uma análise exploratória:
## Series: matter3_ts
## ARIMA(1,0,0) with non-zero mean
##
## Coefficients:
## ar1 mean
## 0.2677 8.3267
## s.e. 0.0504 0.2826
##
## sigma^2 estimated as 15.75: log likelihood=-1020.04
## AIC=2046.09 AICc=2046.15 BIC=2057.782) Análise de dados de Potencial Hidrogeniônico (pH) coletados pelo Departamento de Recursos Hídricos do estado da Califórnia - EUA
Contextualização do problema:
O potencial Hidrogeniônico (pH) é uma variável importante no monitoramento da qualidade da água, uma vez que ele afeta o metabolismo de várias espécies aquáticas. De um modo geral, para a proteção da vida aquática, o pH deve estar entre 6 e 9. Tomou-se o conjunto de dados Potencial Hidrogeniônico (pH), obtido junto ao Departamento de Recursos Hídricos do Estado da California, EUA. A série histórica é constituída por 72.570 observações registradas a cada 15 minutos, de 9/mar/2012 a 9/jun/2014.
O objetivo é realizar uma análise exploratória desta série temporal dada por \(X_{t}\) no intraday.
item i)
Dados brutos antes do tratamento:
Dados após tratamento:
Plot da série temporal \(X_{t}\):
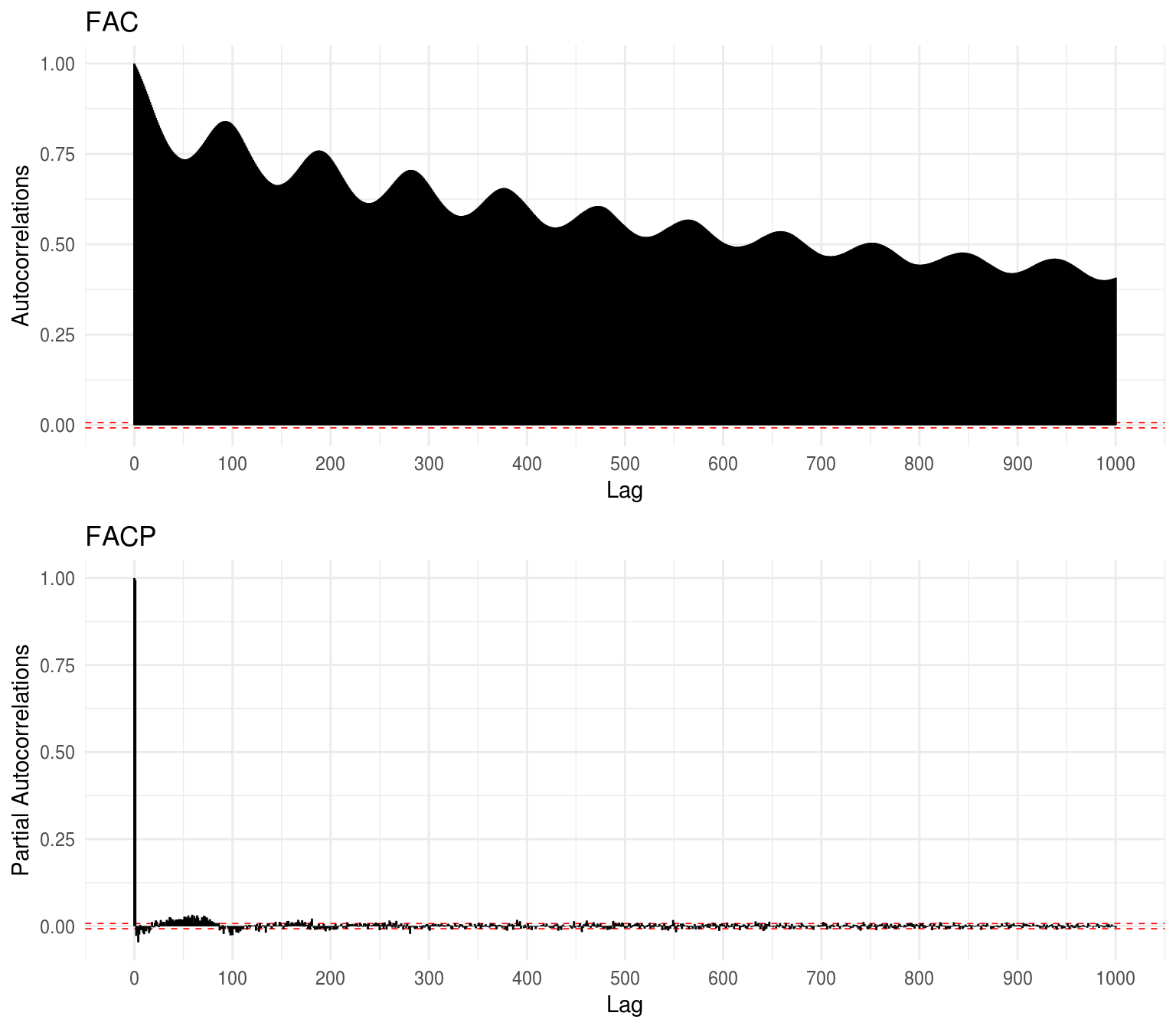
Plots da FAC e FACP:
item ii)
No gráfico da Função de Autocorrelação (FAC/ACF), a qual apresenta comportamento cíclico, o fato de \(\rho(1) \sim 1\) implica um comportamento de quase passeio aleatório \((X_t \sim X_{t-1})\), indicando, assim, a inexistência de estacionariedade na série. Há também um decaimento bastante lento das correlações conforme se avança no tempo, o que também contribui para a violação das condições de estacionariedade. Portanto, há evidências de que a série em análise não seja estacionária.
Há algumas técnicas que podemos empregar para transformar uma série não-estacionária em estacionária. Shumway & Stoffer (2011, pp. 45-47) enumeram: detrending por meio da remoção de uma posível tendência na série temporal; differenciating que consiste em fazer subtrações sucessivas da série sobre ela mesma em um ou mais períodos anteriores; e transformações como \(log(x_{t})\) e Box-Cox. Os próprios autores indicam que, se objetivo é obter a estacionariedade, a opção mais adequada é diferenciar a série. O mesmo propõe Moretin (2005, pp. 4-5), acrescentando ainda, que na maioria das vezes são necessárias apenas uma ou duas diferenças para tornar a série estacionária. Portanto, com base nestes argumentos, empregaremos a diferenciação de primeira ordem na série em questão.
Plot da série após primeira diferenciação:
Com base no gráfico acima, é possível dizer que a série não aponta claros indícios de comportamento não-estacionário, pelo menos com relação a sua média. No entanto, faremos os plots da FAC e FACP a fim de confirmar este resultado.
Plots da ACF e PACF:
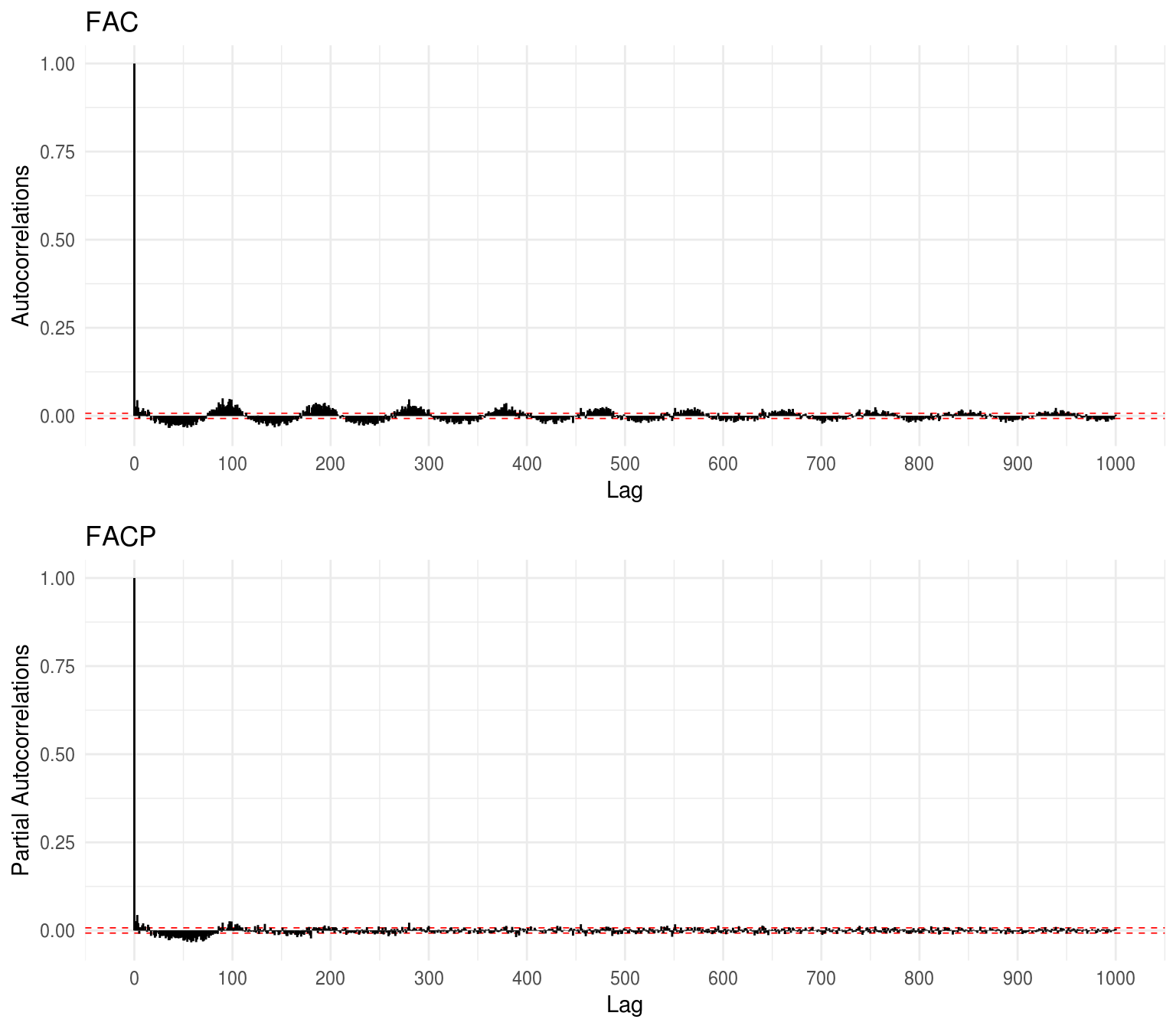
Mesmo com a diferenciação de primeira ordem na série, embora a FAC apresente \(\rho(1)\) bem próximo de zero, as autocorrelações nos lags superiores, de forma ainda cíclica, superam as bandas de confiança e parecem tender de forma bem lenta a zero. Isso nos leva a indicar uma possível ausência de estacionariedade na série. Por este motivo, realizaremos mais uma diferenciação da série na tentativa de obter um comportamento mais compatível com aquele de uma série estacionária.
Plot da série após segunda diferenciação:
Plots da FAC e FACP:
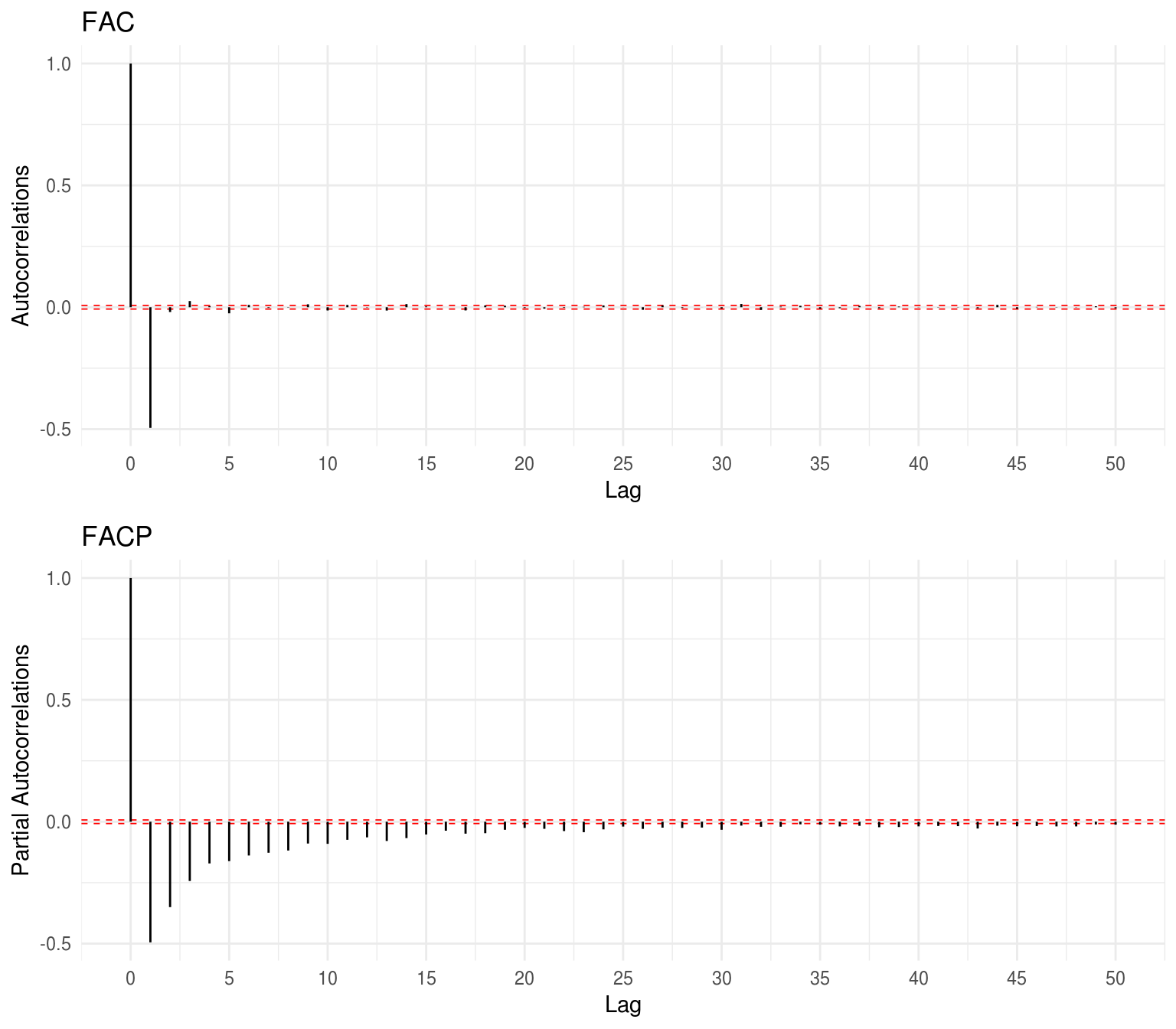
Com \(|\rho(1)| \le 0.5\) no lag \(1\) e o decaimento rápido da Função de Autocorrelação nos lags superiores, temos um forte indicativo de estacionariedade na série. Outros lags além de \(h=3\), cujos valores das autocorrelações por ventura ultrapassam as bandas de confiança, podem ser atribuídos ao percentual esperado de erro tipo I ou ser considerados valores espúrios devido ao erro amostral.
item iii)
Com base na FAC da série original, claramente constata-se a existência de um ciclo na série. Pode-se dizer que os ciclos de correlações positivas e negativas se alternam a cada 50 lags aproximadamente. Levando em consideração que a série apresenta uma periodicidade intraday de 15 em 15 minutos, estes ciclos equivalem, em horas, a:
\[\frac {15 \times 50} {60} = 12.5\]
Portanto, temos ciclos de aproximadamente \(12,5\) horas nos dados, o que provavelmente indica variações de pH que ocorrem ao se alternar entre o período diurno e noturno de cada dia.
item iv)
Tendo em vista a queda abrupta das correlações no gráfico da FAC, no qual temos os 3 primeiros lags com correlação acima das bandas de confiança, e com base também na FACP, que apresenta queda exponencial, sugere-se um modelo de médias móveis ARIMA(0,2,3) para os dados em análise.
3) Análise de dados do índice Dow Jones Industrial da bolsa de valores de Nova Iorque
Contextualização do problema:
Os dados referem-se ao índice Dow Jones Industrial da Bolsa de Valores de Nova Iorque, de 18/9/2009 a 25/05/2010, dispostos numa periodicidade intraday de 1 minuto. As colunas do arquivo de dados, além das datas e dos horários, representam, respectivamente, abertura, máxima, mínima, fechamento e volume.
item i)
Dados brutos antes do tratamento:
Dados após preparação:
Plots das séries DJI: